《数据结构》知识总结

参考视频：速成数据结构与算法-【期末不挂科】_哔哩哔哩_bilibili

数据结构和算法

1.数据结构

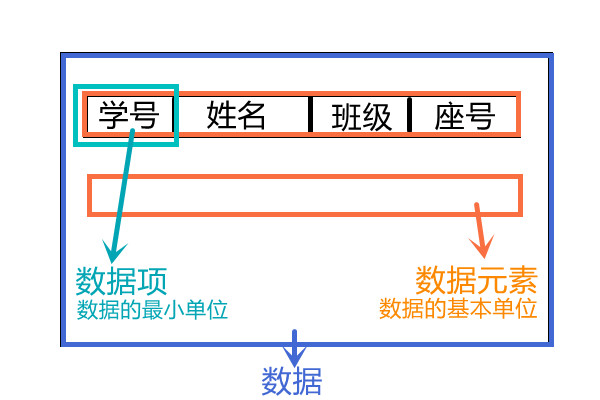
1）数据: 对客观事物的符号表示图像、声音等

2）数据元素: 数据的基本单位学生的信息记录

3）数据项: 构成数据元素的不可分割的最小单位

一个数据元素可由若干个数据项组成学号、姓名、性别等

(4）数据对象: 具有相同性质的数据元素的集合
(5）数据结构: 相互之间存在一种或多种特定关系的数据元素的集合

逻辑结构、存储结构和数据的运算
Data_ Structure=(D,S)

自我理解如图

例题如下

逻辑结构

逻辑结构分为线性结构和非线性结构，其中非线性结构还分有集合、树形结构、图形结构或网状结构

例题：

存储结构

存储结构【区别于存取】大致有：顺序存储、链式存储、索引存储、散列存储

在顺序存储、链式存储、索引存储和散列存储这4种存储方式中，最基本、最常用的两种存储结构是顺序结构、链式结构

算法

算法是对特定问题求解步骤的一种描述

特性

算法应该具有的以下特性

(1）有穷性有穷步骤有穷时间

(2）确定性

(3）可行性

(4）输入一个算法有零个或多个输入

(5）输出一个算法有一个或多个输出

【例题】

以下不属于算法特性的是（)

A.可行性
B.输入
C.确定性
D.健壮性

通常设计一个“好”的算法应考虑达到以下目标:

(1）正确性

(2）可读性

(3）健壮性

(4）效率与低存储量需求

复杂度

算法效率的度量是通过时间复杂度和空间复杂度来描述的频度该语句在算法中被重复执行的次数

算法中所有语句的频度之和T(n)=O(fn))

若一个算法中的语句频度之和为T(n)=n＋4n log2n，则算法的时间复杂度为O(nlog2n)
加法规则:
$$
T(n)=T(n)＋T,(n)=O(f(n))+O(g(n))=O(max (f(n),g(m)))
$$
乘法规则:
$$
T(n)=T (n)×T,(n)=O(f(n))×O(g(n))=O(f(n)×g(n))
$$
常见的渐近时间复杂度为
$$
O(1)<O(log2n)<O(n)<O(nlog2n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)
$$
【例题】

线性表

定义

线性表：具有相同数据类型的n(n≥0)个数据元素的**有限序列**
$$
L=(a,a₂,…,a，aᵢ₊₁，…，aₙ)
$$
除第一个元素外，每个元素有且仅有一个直接前驱

除最后一个元素外，每个元素有且仅有一个直接后继

线性表的基本操作

线性表的基本操作:

InitList(&L);			//初始化表
Length(L);				//求表长
LocateElem(L,e);		//按值查找操作
GetElem(L,i);			//按位查找操作
ListInsert(&L,i,e);		//插入操作
ListDelete(&L,i,&e);	//删除操作
PrintList(L);			//输出操作
Empty(L);				//判空操作
DestroyList(&L);		//销毁操作

线性表的结构

线性表采用顺序存储结构表示时,必须占用一片连续的存储单元

顺序表是由一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻

如果一个顺序表中第一个元素的存储地址为1000,每个元素占4个地址单元，那么第6个元素的存储地址应是（)

A.1020
B.1010
C.1016
D.1024
$$
LOC(A)+sizeof (ElemType)*(i-1)
$$
1
1000＋(6—1)*4=1020

顺序表的特点

顺序表的特点:
(1)顺序表最主要的特点是随机存取，即通过首地址和元素序号可在时间O(1)内找到指定的元素

(2)顺序表的存储密度高，每个结点只存储数据元素

(3)顺序表逻辑上相邻的元素物理上也相邻，所以插入和删除操作需要移动大量元素

顺序表的实现

【例题】在长度为n的顺序表的第i个位置上插入一个元素(1≤i≤n＋i)，元素的移动次数为（ )

A. n - i＋1
B. n - i
C. i
D. i - 1

【例题】设顺序线性表中有n个数据元素，则删除表中第i个元素需要移动（）个元素

A. n - i
B. n - i - 1
C. n - i＋1
D. i

【例题】题3.对于顺序存储的线性表，访问结点和增加、删除结点的时间复杂度为（ )

A. O(n),O(n)
B. O(n),O(1)
C. O(1),O(n)
D. O(1),0(1)
顺序表最主要的特点是随机存取，即通过首地址和元素序号可在时间O(1)内找到指定的元素
增加、删除结点的时间复杂度为O(n)

链表

单链表的结构

单链表:链式存储的线性表

不带头结点

带头结点

【例题】

单链表的实现（操作）

实现代码如下

LNode *GetElem(LinkList L,int i){		//LNode结点类型，函数名为GetElem，单链表L,查找第几位数（要求返回第ai位的值）
	int j=1;							//计数用
	LNode *p=L->next;					//设置指针p为第一个结点（L头结点的下一个结点是a1）
    if(i==0)	return L;				//如果i=0，返回L值
	if(i<0)		return NULL;			//如果i<0，返回错误
	while(p&&j<i){						//p的值为是否为空&&j是否超过i
	p=p->next;	j＋+;					//指针往下
	}
	return p;							//p的值为为空（i定义过大）或 j等于i（找到），返回p所指的ai位记录的值
}

时间复杂度为O(n)

【例题】

插入结点

实现插入结点的代码如下:

1
2
3

p=GetElem(L,i-1);
s一>next=p一>next;
p->next =s;

【例题】

按照一步一步操作，选B，

删除结点

实现删除结点的代码片段如下:

p=GetElem (L,i—1);
q=p->next;			//定义q为p的下一个
p->next=q->next;	//把q的下一个（c）作为p的下一个
free(q);			//释放q

双链表

双链表比单链表多了前驱（prior）指针，指向前面一个元素

插入操作

s->next = p->next;	//让x的下一个给b（p->next）
p->next->prior = s;	//让b（p->next）的前驱为x
s->prior = p;		//让x的前驱为a
p->next = s;		//让p的后续为x

上述代码不唯一，但是第一行代码和第二行代码必须在第四行之前

删除操作

代码如下

1
2
3

p->next=q->next;	//让p的后续等于c（q->next）
q->next—>prior=p;	//让c的前驱（q->next—>prior）指向p
free(q);			//释放q

循环列表

【例题】

由于

所以本题选C

栈和队列

栈

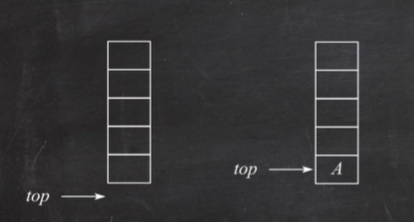
栈:只允许在一端进行插入或删除操作的线性表
栈顶栈底

初始化

Status lnitStack(SqStack &s ,int MAXSIZE ){

S. base =new SElemType[MAXSIZE];

if( !S. base ) return OVERFLOW;

S.top = S. base;

S.stacksize = MAXSIZE;

return OK;
}

空栈:不含任何元素的空表

特性:先进后出

限定仅在表尾进行插入和删除操作的线性表称为栈 ,它的修改是按先进后出的原则进行的

【例题】若进栈序列为a,b,c，则通过入栈操作可能得到的a,b,c出栈的不同排列个数（)
A.4 B.5 C.6 D.7

n个不同元素进栈,出栈元素不同排列的个数为

所以选B.5

栈的存储结构

顺序栈的实现

栈的顺序存储类型可描述为:

#define MaxSize 50
typedef struct {
  ElemType data[MaxSize];
  int top;
} SqStack;

顺序栈的基本运算

1.初始化

1
2
3

void InitStack (SqStack &S){
S.top = -1;
}

2.判栈空

bool StackEmpty (SqStack &S){
if(S.top == -1)
  return true;
else
  return false;
}

3.进栈：栈不满时，栈顶指针先加1，再送值到栈顶元素

bool Push(SqStack &S, ElemType x){
  if(S.top == MaxSize-1)
    return false;
  S.data[++S.top]=x;
  return true;
}

或

Status Push( SqStack &s, SElemType e)

{ 
  if( S.top - S.base== S.stacksize )
    return ERROR;
  *S.top++=e;
  return OK;
}

4.取栈顶元素:

Status Pop(SqStack &S,SElemType &e)
{
  if( S.top == S.base ) //栈空
  return ERROR;
  e=*--S.top;			//e为原指针下一个，并且原指针--
  return OK;}

5.求栈长度:

int StackLength( SqStack S ){
  return(S.top - S. base) ;
}

链栈

队列的基本概念

队列: 队，只允许在表的一端进行插入，而在表的另一端进行删除
入队或进队
出队或离队
特性: 先进先出

题1.队列是一种操作受限的线性表,它与栈不向的是,队列中所有的插入操作均限制在表的一段进行，而所有的删除操作都限制在表的另一端进行,允许插入的一端称为队尾，允许删除的一端称为对头（对首），队列具有先进先出的特点